4 Coloring Np Complete
13072006 2014 The NP-completeness of Eulerian Recurrent Length for 4-regular Eulerian Graphs. 4-COLOR is in NP.

Pdf The Np Completeness Of Edge Coloring Semantic Scholar
If all checks pass accept.

4 coloring np complete. Many graph coloring algorithm such as the Saturation algorithm the Recursive Largest First algorithm Simulated Annealing. Let C be an instance of 3-SAT with clauses C 1 C 2 C m and variables x 1 x 2 x n. Given a graph G.
To your problem in some way. Though if you can prove that it is youve just won 1000000. K -coloring is NP-complete for k 3.
4-SAT problem is in NP. Color each node of as specified by. 2014 4th International Conference on Artificial Intelligence with Applications in Engineering and Technology 155-159.
It is NP-complete to decide if a given graph admits a k-coloring for a given k except for the cases k 012. 3 Show that Y P X. LOCAL 4-COLORING is NP-complete.
For each node check that it has a unique color from each of its neighbors. You just go through all the patches check that the neighbors are of different color and finally count the total number of colors. Check that includes _dh colors.
14102020 Thus it can be verified that the 4-SAT Problem is NP-Complete using the following two propositions. I will help you to solve this question. Prove that 4-COLOR is NP-complete.
Every variable has one of two values. The following is a verifier g for 4-COLOR. If any problem is in NP then given a certificate which is a solution to the problem and an instance of the problema formula f in this case it can be verifiedcheck whether the solution given is correct or not that the certificate in polynomial time.
Show that 4-COLOUR is NP-Complete using the fact that 3-COLOUR is NP- complete. My thinking was to essentially prove a bi-conditional. Do this by showing there is an certi cate that can be e ciently checked.
10122007 We show that deciding if a graph without induced paths on nine vertices can be colored with 4 colors is an NP-complete problem improving a previous NP-completeness result proved by Woeginger and Sgall in 2001. We also finished the proof that finding Hamiltonian paths is hard. Planar graphs are 4-colorable.
Create triangle with node True False Base for each variable x i two nodes v i and v i connected in a triangle with common Base If graph is 3-colored either v i or v i gets the same color as True. Stated but unproven results. 21042016 I am trying to show that the NP-Complete problem of 3-coloring a graph reduces to the problem of 10-coloring a graphI have already shown how 10-coloring can be verified in polynomial time and is thus in NP.
Endgroup Misha Lavrov May. 1 Must show that X 2NP. The complexity of 4-coloring graphs without induced paths on five vertices remains open.
The coloring is the certificate ie a list of nodes and colors. The resulting graph is denoted by H i. Coloring problem is known to be NP-complete 412 there is no known algorithm which for every graph will optimally color the nodes of the graph in a time bounded by a polynomial in the number of nodes.
Interpret this as a truth assignment to v i For each clause C j abc create a small gadget graph. The 3-coloring problem remains NP-complete even on 4. Two adjacent vertices are in conflict if they have the same color I want to prove the above problem is NP-complete.
Following the same reasoning 5-Coloring 6-Coloring and even general k-Coloring problem can be proved NP-Complete easily. For each clause C i i 1 2 m take a copy of the clause gadget graph H and remove vertices α 1 α 2 α 3 and their incident edges. This algorithm scales linearly with the number of regions so it is a.
It would seem that 2COLOR whether a graph has a 2-coloring would be a better fit. Every questions wilth NP Complete is interesting. N via colors for some nodes in Gφ.
We will prove it by two steps. Graph coloring is computationally hard. In particular it is NP-hard to compute the chromatic number.
Interestingly 2COLOR is known to be in P and is conjectured not to be NP-complete. 27052019 If you had an algorithm to solve 4-coloring you could use it to test if a graph G is 3-colorable by adding a vertex adjacent to all others and testing if the new graph G is 4-colorable. Given a graph G V E and an integer K 3.
G On input 1. Here is the answer. As a consequence 4-Coloring problem is NP-Complete using the reduction from 3-Coloring.
Reduction from 3-Coloring instance. For a check you are given with a particular coloring of the given map. Since 3-colorability is NP-complete all NP problems can be reduced to 3-coloring and then we can use this strategy to reduce them all to 4-coloring.
Given a graph G V E and a set of colors k. A K-coloring problem for undirected graphs is an assignment of colors to the nodes of the graph such that no two adjacent vertices have the same color and at most K colors are used to complete color the graph. Adding an extra vertex to the graph of 3-Coloring problem and making it adjacent to all the original vertices.
Why Not Two Colors. This has been added to last lectures notes. Find a assignment of colors to vertices that minimizes the number of adjacent vertices in conflict.
Now I just need to show it indeed can be reduced to 3-coloring. General Strategy for Proving Something is NP-complete. Every node has one of two values.
2 Look at some problems that are known to be NP-complete there are thousands and choose one Y that seems similar.

National Park Coloring Books Great For Both Junior And Not So Junior Rangers Cat Coloring Coloring Books Cat Coloring Page

Np Completeness 3 Color Thu Oct 27 12 53 Pm Youtube

Fall Grid Coloring Pages Mystery Picture Activities Woo Jr Kids Activities Mystery Pictures Math Coloring Pixel Art Grid
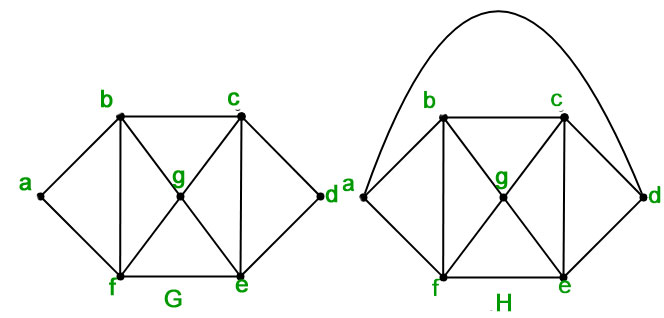
Mathematics Planar Graphs And Graph Coloring Geeksforgeeks
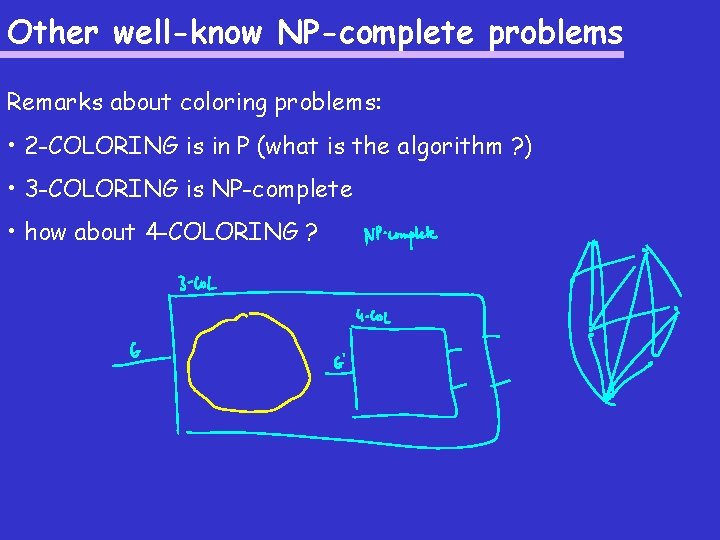
Polynomialtime Reductions We Have Seen Several Reductions Polynomialtime
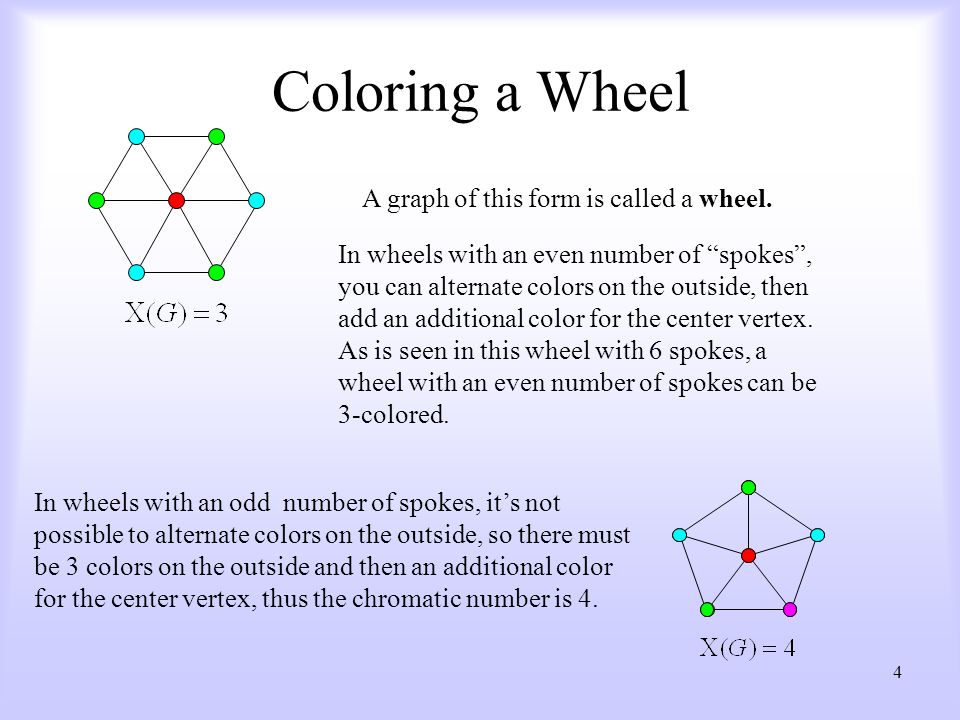
Graph Coloring Ppt Video Online Download
Pdf The Np Completeness Of Edge Coloring Semantic Scholar

Essential Balance Nippon Paint Singapore Nippon Paint Painting Services Exterior Paint

4 Honda Accord Ex Engine Diagram Honda Accord Ex Honda Accord Engine Diagram