K Coloring Algorithm

Giant at April 20, 2021

The chromatic number of. An edge coloring of a graph is a proper coloring of the edges meaning an assignment of colors to edges so that no vertex is incident to two edges of the same color.

Graph Coloring Ppt Video Online Download

The K-1 Coloring algorithm assigns a color to every node in the graph trying to optimize for two objectives.

K coloring algorithm. To use as few colors as possible. That was Kempes simplest algorithm to 6-color a planar graph. 14112013 Basic Greedy Coloring Algorithm.

In general the algorithm does not give the lowest k for which there exists a k-coloring but tries to find a reasonable coloring. The input graph G with a proper 3 -coloring of its vertices found by the algorithm. 5-color a planar graph.

Pseudo code for canColor. Color first vertex with first color. An edge coloring with k colors is called a k-edge-coloring and is equivalent to the problem of partitioning the edge set into k matchings.

If all previously used colors. The adaptive memory algorithm is a hybrid evolutionary heuristic that uses a central memory. A greedy algorithm for finding a non-optimal coloring Here we will present an algorithm called greedy coloring for coloring a graph.

K3 shown below in figure 32 with 12 vertices 11 12 13 21 22 23 31 32 33 41 42 43. E 3 e 6 Step 2- After coloring the edges in Fig1 we arrive at the graph in Fig2 Step 3- Remaining colors are c 4 and c 5 Step 4- After coloring the vertices with the remaining colors c 4 and c 5 we arrive at the graph in Fig3. Do following for remaining V-1 vertices.

To use as few colors as possible. 22012014 The greedy coloring algorithm assigns a color non-negative integer cx to each vertex xin a greedy manner as follows. Let us color the graph using the algorithm.

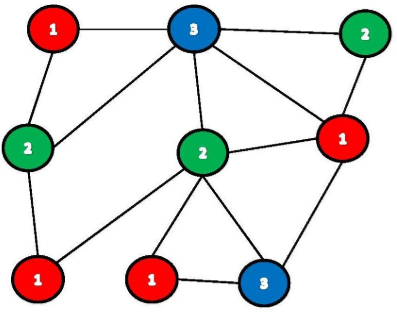
To make sure that every neighbor of a given node has a different color than the node itself. 15012008 The k -coloring problem is to assign a color a number chosen in 1 k to each vertex of G so that no edge has both endpoints with the same color. The problem states that given m colors determine a way of coloring the vertices of a graph such that no two adjacent vertices are assigned same color.

Step 1- Independent set of edges are e 1 e 4. Vertex coloring is the most commonly encountered graph coloring problem. Wigderson Algorithm is a graph colouring algorithm to color any n-vertex 3-colorable graph with On colors and more generally to color any k-colorable graph.

06052015 First lets define the problem canColorgraph k - it will answer true if and only if you can do a graph coloring to graph using k colors. The smallest number of colors needed for an edge coloring of a graph G is the. A k-coloring of a graph is an assignment of one of k distinct colors to each vertex in the graph so that no two adjacent vertices are given the same color.

Algorithms Wigderson Graph Colouring Algorithm in ONM time. E 2 e 5. 0 k 0 1 for i 1 to ndo 2 let ci be the smallest positive integer such that.

Algorithm 2 Kuhn-Wattenhofer color-reduction algorithm 1 function KWColorReductionG VE n jVj for v 1ndo in parallel c v v end for k unique elements in fc v. Or in general to K-color a graph in class C such that 1 every graph in class C has a node of degree K and 2 removing a node from a graph in class C gives you another graph in class C. 1 do Divide colors into bins of size 2 1 Let each bin be denoted as G i V iE i.

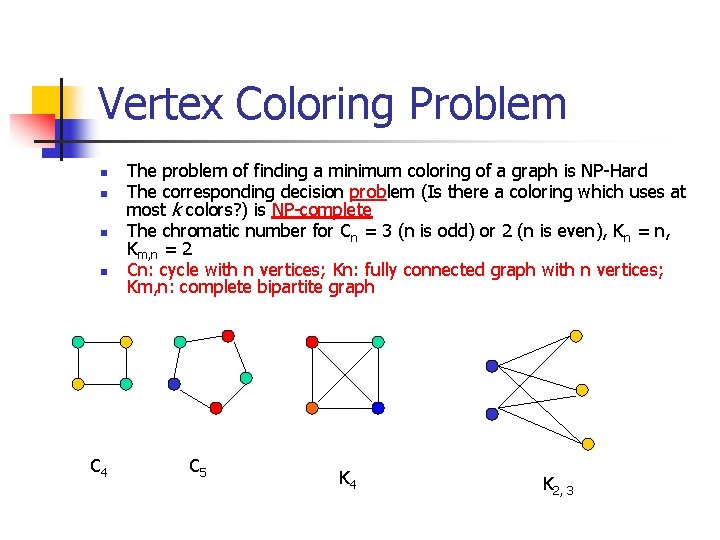
The smallest number of colors needed to color a graph G is called its chromatic number. The variable kstores the number of colors used. Given a graph G V E and an integer K 3.

For ido in parallel ColorReductionG i V iE i k k 1 end for end while end function Starting with the n-coloring. This will be the output. Return checkIfColoringValidgraph v first uncolored vertex for each i from 1 to k inclusive color v with color i can add optimization here to trim upfront unsuccesful.

To make sure that every neighbor of a given node has a different color than the node itself. Kempe had two more algorithms. A K-coloring problem for undirected graphs is an assignment of colors to the nodes of the graph such that no two adjacent vertices have the same color and at most K colors are used to complete color the graph.

If graph is completely colored. The algorithm first constructs the Cartesian product G. A Consider the currently picked vertex and color it with the lowest numbered color that has not been used on any previously colored vertices adjacent to it.

The K-1 Coloring algorithm assigns a color to every node in the graph trying to optimize for two objectives. Adji is the list of vertices adjacent to vertex i. In this article we have explored this wonderful graph colouring article in depth.

Graph Coloring Algorithm Youtube