2 Coloring Np Complete
Given a graph GVE the colouring problem asks for an assignment of kcolours to the vertices c. Any k-D2-edge-colorable graph is also k 1-D2-edge-colorable.
Now consider the 2-Colorig problem where we only have two colors say red and blue and each vertex must have a different color than its neighbors in order for the 2- Coloring.

2 coloring np complete. Graph Coloring is NP-complete 3-Coloring 2NP. Whats the colouring problem on graphs. Let us consider now equitable vertex coloring of.
Every variable has one of two values. Determining whether a bipartite graph with girth 6 and maximum degree 3 is 5-D2edge-colorable is NP-complete. For each node a color from 123 Certifier.
14112013 We introduced graph coloring and applications in previous post. On the other hand the Graph Coloring Optimisation problem which aims to find the coloring with minimum colors is. 28042004 distinct colors in such a way that no two adjacent vertices are colored the same color.
What is vertex coloring of a graph. 02122016 Since 2-coloring is in NP and we dont know if there is a reduction of any NP-complete to 2-color. Introduction to Complexity Theory.
Unfortunately for k 3 the problem is NP-complete. We present a new proof that shows that the strong edge. We prove that it is NP-complete to determine whether there exists a distance-2 edge coloring strong edge coloring with 5 colors of a bipartite 2-inductive graph with girth 6 and maximum degree 3.
Unfortunately I havent found a for me reasonable and clear proof. 3-Colouring is NP-complete We next show that 3-colouring is NP-complete. We say that a colouring is proper if adjacent vertices receives di erent colours.
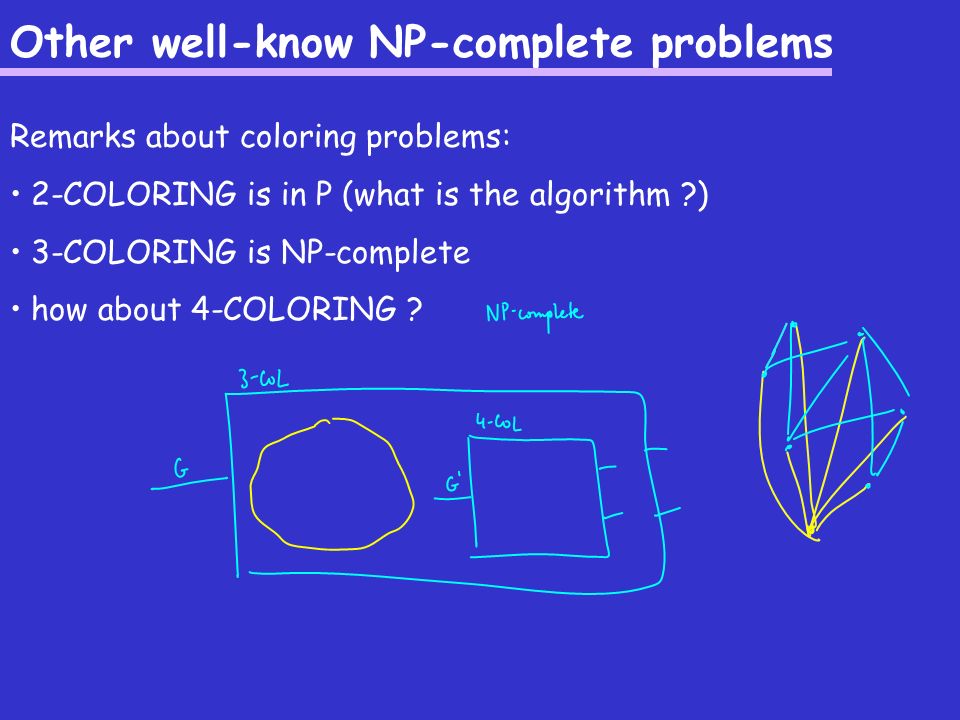
Recall that the 3-Coloring problem is NP-Complete as we have proven in class. We will show 3-SAT P 3-Coloring. The Graph Coloring decision problem is np-complete ie asking for existence of a coloring with less than q colors as given a coloring it can be easily checked in polynomial time whether or not it uses less than q colors.
NP-Completeness Graph Coloring Graph K-coloring Problem. As discussed in the previous post graph coloring is widely used. Check out the course here.
Prove that 4-COLOR is NP-complete. A A condition where any two vertices having a common edge should not have same color b A condition where any two vertices having a common edge should always have same color. Vertex k-Coloring is NP-complete when restricted to graphs of the form G N 1 while χ G N 1 can be found in polynomial time.
A K-coloring problem for undirected graphs is an assignment of colors to the nodes of the graph such that no two adjacent vertices have the same color and at most K colors are used to complete color the graph. Unfortunately there is no efficient algorithm available for coloring a graph with minimum number of colors as the problem is a known NP Complete problemThere are approximate algorithms to solve the problem though. To prove NP-hardness we describe a reduction from Not-All-Equal-3SAT.
The coloring is the certificate ie a list of nodes and colors. The following is a verifier g for 4-COLOR. 4-COLOR is in NP.
Determining if a graph is a cycle or is bipartite is very easy in L but finding a maximum bipartite or a maximum cycle subgraph is NP-complete. Discrete Applied Mathematics 160 18 2681-2693. Theorem 3-Coloring is NP-complete.
2012 b-coloring of tight graphs. It is known that Vertex k-Coloring of a general graph is NP-complete for k 3 and remains so also for graphs of type G N 1 and k 4. Check if for each edge uv the color of u is different from that of v Hardness.
If a problem solvable in linear time turned out to be NP-hard that. In class we learned that 2-COLOR P and 3-COLOR is NP-complete. Why Not Two Colors.
I tried to reduce the 4-coloring problem to the 3-coloring problem and since that is NP-complete the 4-coloring problem would be NP-complete. This video is part of an online course Intro to Algorithms. Interestingly 2COLOR is known to be in P and is conjectured not to be NP-complete.
Mahdian 2 3 proved via a reduction from Graph k-colorability that it is NP-complete to determine for every fixed g whether a bipartite graph with girth g has a strong edge coloring with k colors for k 4. If PNP then the answer is no. Special case of k 2 How can we test if a graph has a 2-coloring.
The problem is clearly in NP since a coloring can be verified in polynomial time. It would seem that 2COLOR whether a graph has a 2-coloring would be a better fit. I know that the 4-coloring problem is NP-complete but Im looking for a proof of that statement.
Check if the graph is bipartite. 3-Coloring is NP-Complete 3-Coloring is in NP Certificate. If PNP then the answer is almost certainly not.
Calculating the chromatic number of a graph is an NP complete problem as a chromatic number of an arbitrary graph. 13072006 2012 The P versus NPcomplete dichotomy of some challenging problems in graph theory. Determining whether a graph can be colored with 2 colors is in P but with 3 colors is NP-complete even when restricted to planar graphs.
Though if you can prove that it is youve just won 1000000. Given a graph GV E and an integer K 3 the task is to. A valid coloring gives a certi cate.
G On input. Every node has one of two values. A distance-2-edge-coloring is also known as a strong edge coloring.
2-colouring is not only in P there is a linear-time algorithm on a random access machine. We will show that.

Pdf Coloring The Maximal Cliques Of Graphs

Alphabet Maze English Unite Alphabet Worksheets Preschool Phonics Worksheets Abc Worksheets

3 Coloring Is Np Complete Geeksforgeeks

Pdf The Np Completeness Of Edge Coloring Semantic Scholar
Polynomial Time Reductions We Have Seen Several Reductions Ppt Download
![]()
Pdf Quantum Algorithms For Colouring Of Graphs

Essential Balance Nippon Paint Singapore Ide Dekorasi Rumah Dekorasi Rumah Rumah